Motivation

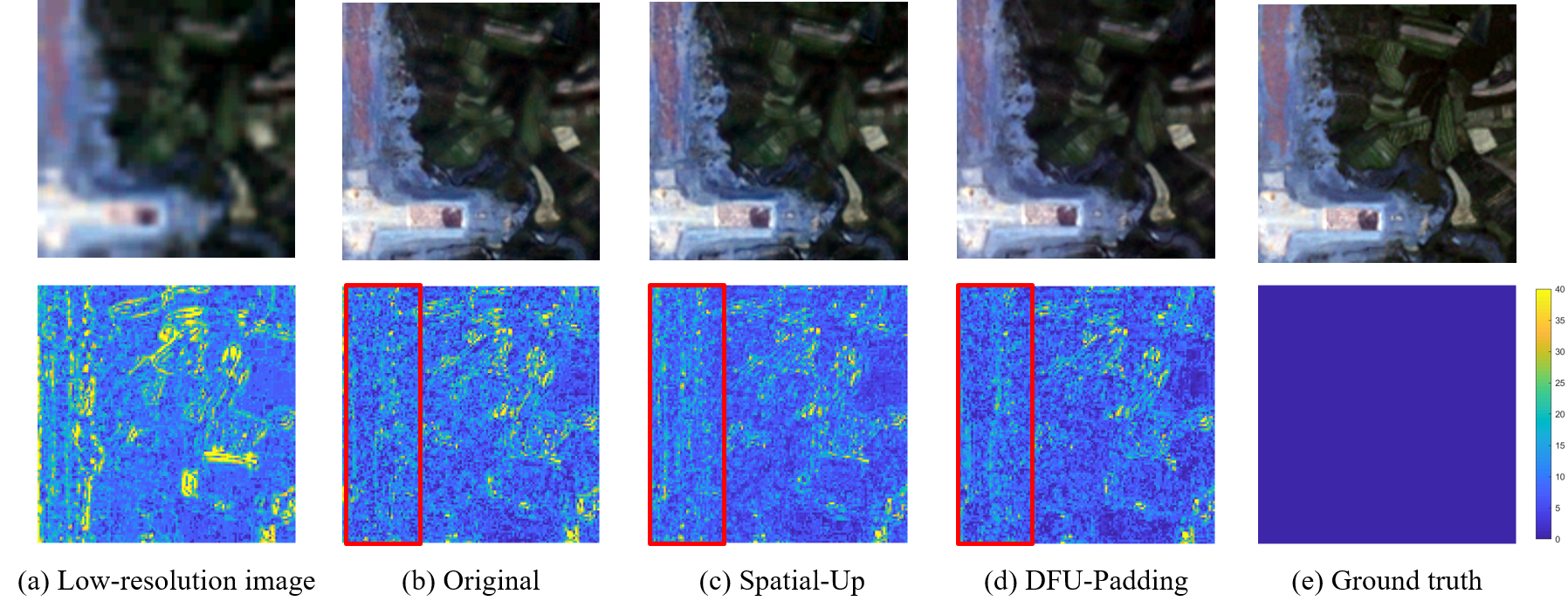
Motivations: (a) and (b) imply that arbitrary up-sampling, interpolation, in the Fourier domain produces sub-optimal result as it does not follow the same local similarity property as that in the spatial domain. This motivates us to design a more ingenious ``Fourier Up-Sampling'' operator, dubbed as FourierUp. It has three alternative variants: Periodic Padding, Area Interpolation/Cropping, and Corner Interpolation.
Abstract
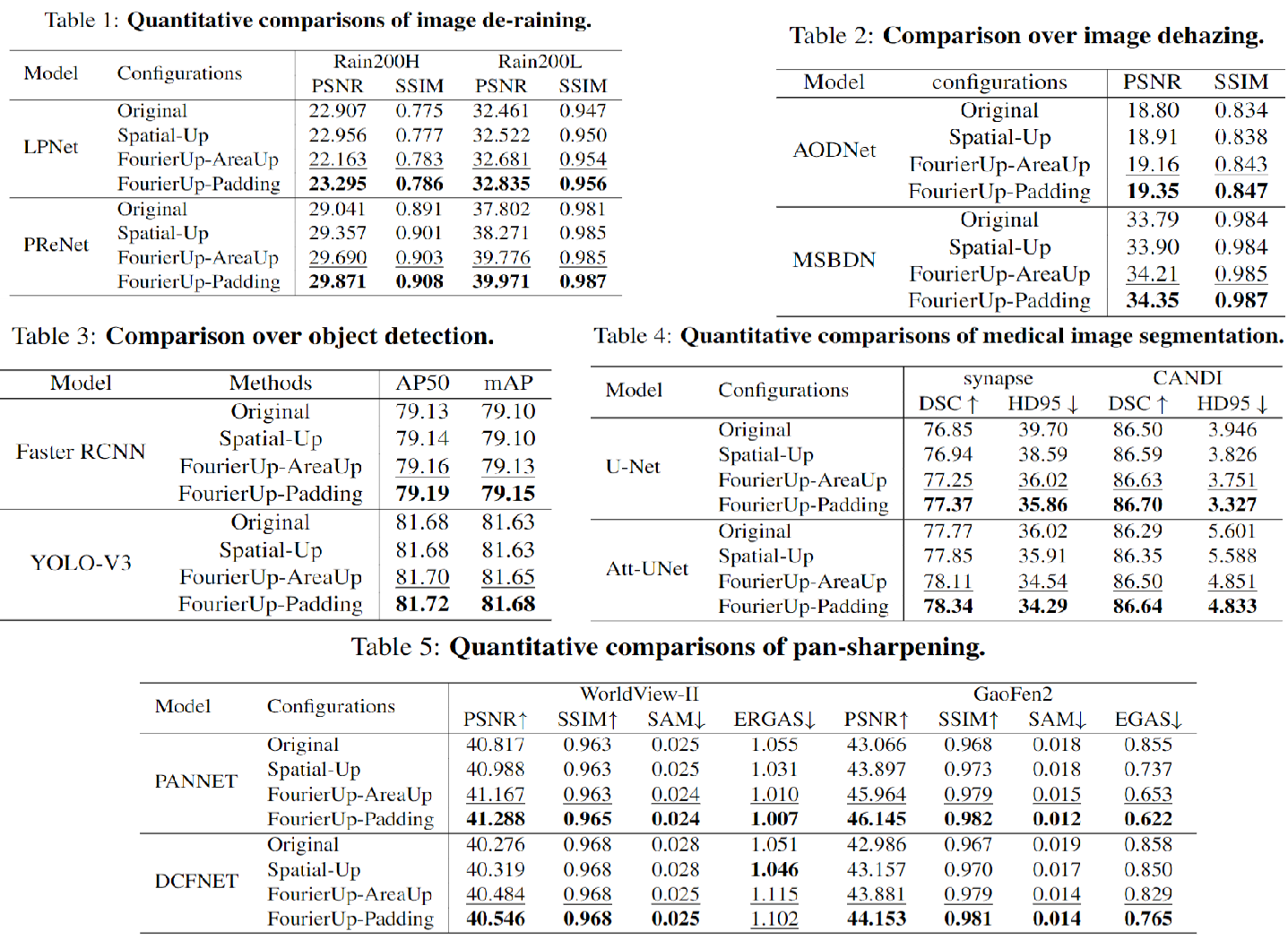
Existing convolutional neural networks widely adopt spatial down-/up-sampling for multi-scale modeling. However, spatial up-sampling operators (e.g., interpolation, transposed convolution, and un-pooling) heavily depend on local pixel attention, incapably exploring the global dependency. In contrast, the Fourier domain is in accordance with the nature of global modeling according to the spectral convolution theorem. Unlike the spatial domain that easily performs up-sampling with the property of local similarity, up-sampling in the Fourier domain is more challenging as it does not follow such a local property. In this study, we propose a theoretically feasible Deep Fourier Up-Sampling (FourierUp) to solve these issues. We revisit the relationships between spatial and Fourier domains and reveal the transform rules on the features of different resolutions in the Fourier domain, which provide key insights for FourierUp's designs. FourierUp as a generic operator consists of three key components: 2D discrete Fourier transform, Fourier dimension increase rules, and 2D inverse Fourier transform, which can be directly integrated with existing networks. Extensive experiments across multiple computer vision tasks, including object detection, image segmentation, image de-raining, image dehazing, and guided image super-resolution, demonstrate the consistent performance gains obtained by introducing our FourierUp. Code is publicly available at
Method
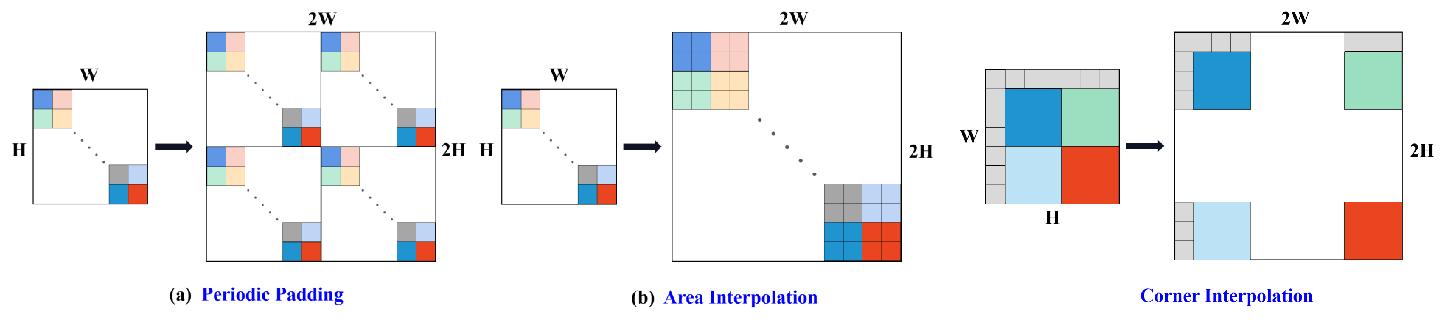
Illustration of the three alternative variants: Periodic Padding, Area Interpolation/Cropping, and Corner Interpolation. Each small color square represents a pixel of the amplitude/phase component in the Fourier domain. The gray parts represent a row/column pixels while the remaining color parts are evenly divided.
Results
License
We retain all the copyrights of this method.
Citation
If you find our dataset and paper useful for your research, please consider citing our work:
@inproceedings{FourierUp,
author = {Zhou, Man and Hu, Yu and Huang, Jie and Zhao, Feng and Gu, Jinwei and Loy, Chen Change and Meng, Deyu and Li, Chongyi},
title = {Deep Fourier Up-Sampling},
booktitle = {},
year = {2022}
}
Contact
If you have any question, please contact us via manman@mail.ustc.edu.cn.